MPO
503: Introduction to Physical Oceanography
Notes:
The last lecture we saw how conservation of potential vorticity governs the evolution of flows in the ocean. What can we learn from vorticity about the steady, large-scale circulation using vorticity?
Sverdrup combined geostrophy with Ekman dynamics to find a powerful relation for the size and pattern of ocean's circulation in response to the winds. We are going to derive Sverdrup's balance by first considering the geostrophic interior and the frictional surface boundary layer (Ekman layer) separately, in order to highlight how these two regimes couple to form an ocean gyre.
1. We start with geostrophy:
Initially, we cross differentiate the u and v momentum equations as we did in last class, but this time we assume a steady state:

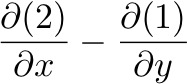
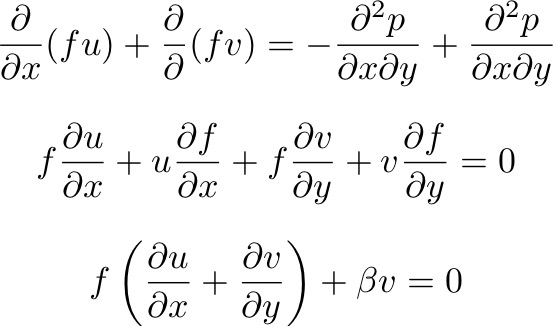
Last
modified: Dec 2014
The last lecture we saw how conservation of potential vorticity governs the evolution of flows in the ocean. What can we learn from vorticity about the steady, large-scale circulation using vorticity?
Sverdrup combined geostrophy with Ekman dynamics to find a powerful relation for the size and pattern of ocean's circulation in response to the winds. We are going to derive Sverdrup's balance by first considering the geostrophic interior and the frictional surface boundary layer (Ekman layer) separately, in order to highlight how these two regimes couple to form an ocean gyre.
1. We start with geostrophy:
Initially, we cross differentiate the u and v momentum equations as we did in last class, but this time we assume a steady state:

Cross-differentiating:
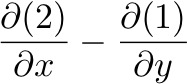
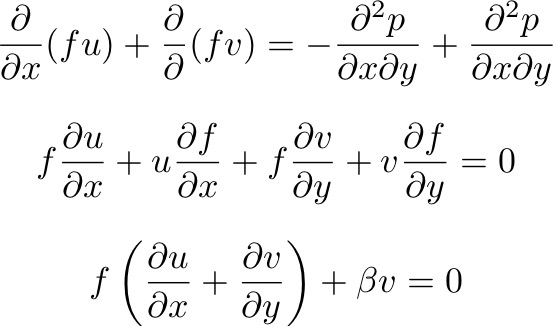
Or:
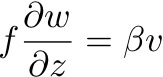
Which is the
geostrophic vorticity equation, where:
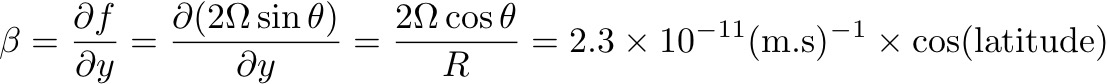
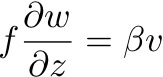
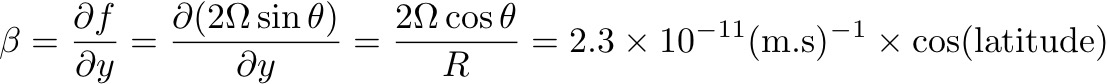
Thus,
β << f
except near the Equator.
So, the divergence of the flow is proportional (at any latitude) to its northward or meridional velocity. How can that be? Remember last class, if you change the thickness of a water column over a rotating sphere, it will need to change its spin to conserve PV. If ζ << f, then the water will move north/south!
[Note: in contrast to f, β is positive in both hemispheres. We will see later that this has the important effect of causing strong currents on the western side of all ocean basins.]
If we vertically integrate the geostrophic velocity balance we find:
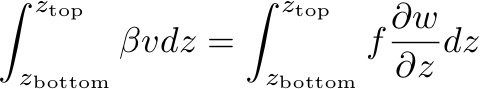
With boundary
conditions w(zbottom)
= 0, w(ztop)
= wtop. Here, zbottom
is the seabed and ztop
is the top of the geostrophic interior. For w(zbottom)
= 0 we are assuming a flat-bottomed ocean.
Then:

Thus, at any latitude, the meridional transport is proportional to the vertical velocity at the top of the geostrophic ocean.
2. Now, let's look at Ekman:

Again we cross-differentiate these equations:
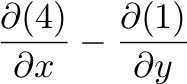

Vertically integrate over the depth of the Ekman layer, using as boundary conditions w(z0) = 0, w(zEk) = wEk:
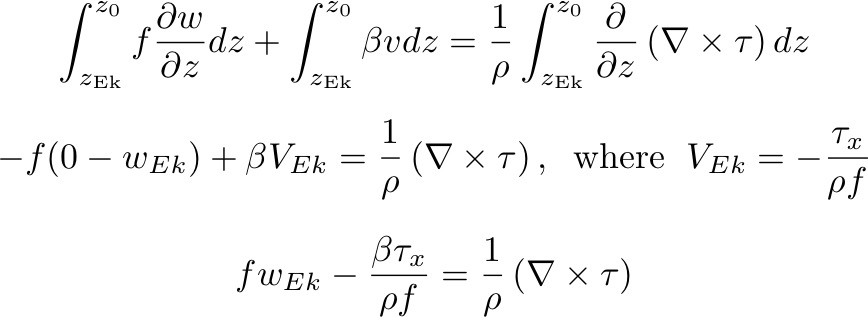
The second term on the left hand side is small except near the Equator, where β > f. The equation then becomes:
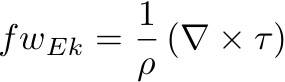
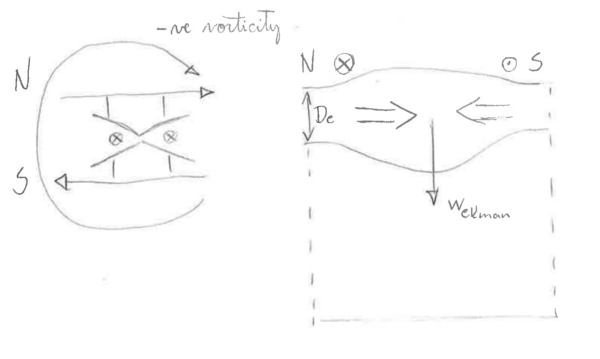
Conversely, for
anticlockwise winds, the Ekman transport is
divergent and the vertical velocity is upward. This
is called EKMAN SUCTION.
3. Combining the geostrophic interior and Ekman layer:
We can combine the Ekman and geostrophic layers very simply by looking at the two vorticity equations we have.

Equating wEk = wtop gives the SVERDRUP BALANCE:
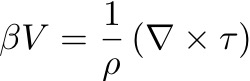
This is a pointwise balance, true for anywhere in the ocean where the following assumptions are valid:
- Flow is steady - d/dt = 0;
- Flow is frictionless below the Ekman layer;
- wbottom is small - "flat bottom assumption".
So, the wind-driven ocean gyres can be though of as two layers:
(1) A surface layer where the curl of the wind field drives convergences and divergences which drive vertical flows (or changes in layer depth).
(2) An interior, geostrophic layer driven by the vertical flows (Ekman pumping/suction) that result from divergent/convergent Ekman transports.
Sverdrup did the entire problem at once, by taking the curl of the momentum equations with the wind stress terms included:
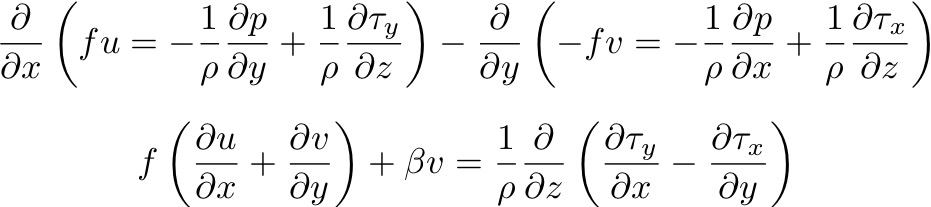 :
:
Vertically integrating from the sea bottom to the sea surface, with boundary conditions w(z = bottom) = 0 and w(z = 0) = 0, gives the Sverdrup balance:
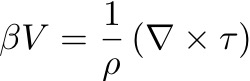
This depth-integrated balance drops the details of the Ekman layer + geostrophic interior physics, to give us the (deceptively) simple result that the WIND STRESS CURL DRIVES THE MERIDIONAL TRANSPORT.
- clockwise (negative) wind stress curl: southward transport.
- anticlockwise (positive) wind stress curl: northward transport.
In terms of vorticity, you can think of it as the input of vorticity from the wind being "stored" in the ocean by moving a column of water to a region with higher or lower planetary vorticity.

So, the divergence of the flow is proportional (at any latitude) to its northward or meridional velocity. How can that be? Remember last class, if you change the thickness of a water column over a rotating sphere, it will need to change its spin to conserve PV. If ζ << f, then the water will move north/south!
[Note: in contrast to f, β is positive in both hemispheres. We will see later that this has the important effect of causing strong currents on the western side of all ocean basins.]
If we vertically integrate the geostrophic velocity balance we find:
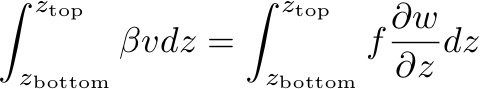
Then:

Thus, at any latitude, the meridional transport is proportional to the vertical velocity at the top of the geostrophic ocean.
2. Now, let's look at Ekman:

Again we cross-differentiate these equations:
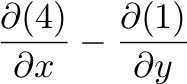

Vertically integrate over the depth of the Ekman layer, using as boundary conditions w(z0) = 0, w(zEk) = wEk:
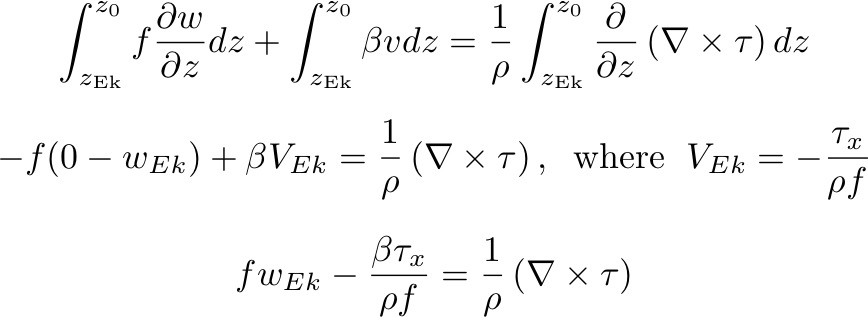
The second term on the left hand side is small except near the Equator, where β > f. The equation then becomes:
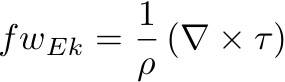
This
states that the vertical velocity at the base of
the wind-driven Ekman layer is proportional to the
curl of the wind stress. For clockwise curl 𝜏,
the left hand side is negative ans so wEk
is downward. This is called EKMAN PUMPING. The
figure on the following
gives an example for the interior of the
North Atlantic subtropical gyre:

3. Combining the geostrophic interior and Ekman layer:
We can combine the Ekman and geostrophic layers very simply by looking at the two vorticity equations we have.

Equating wEk = wtop gives the SVERDRUP BALANCE:
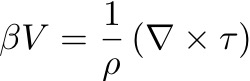
This is a pointwise balance, true for anywhere in the ocean where the following assumptions are valid:
- Flow is steady - d/dt = 0;
- Flow is frictionless below the Ekman layer;
- wbottom is small - "flat bottom assumption".
So, the wind-driven ocean gyres can be though of as two layers:
(1) A surface layer where the curl of the wind field drives convergences and divergences which drive vertical flows (or changes in layer depth).
(2) An interior, geostrophic layer driven by the vertical flows (Ekman pumping/suction) that result from divergent/convergent Ekman transports.
Sverdrup did the entire problem at once, by taking the curl of the momentum equations with the wind stress terms included:
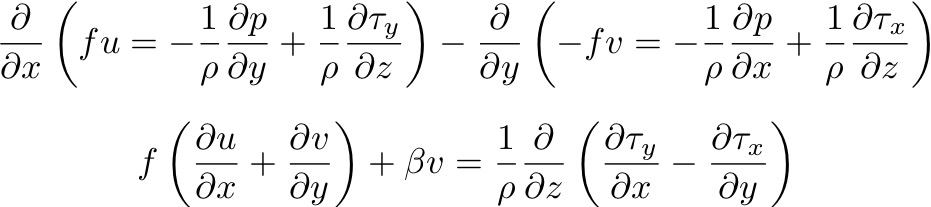 :
:Vertically integrating from the sea bottom to the sea surface, with boundary conditions w(z = bottom) = 0 and w(z = 0) = 0, gives the Sverdrup balance:
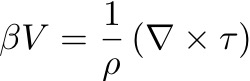
This depth-integrated balance drops the details of the Ekman layer + geostrophic interior physics, to give us the (deceptively) simple result that the WIND STRESS CURL DRIVES THE MERIDIONAL TRANSPORT.
- clockwise (negative) wind stress curl: southward transport.
- anticlockwise (positive) wind stress curl: northward transport.
In terms of vorticity, you can think of it as the input of vorticity from the wind being "stored" in the ocean by moving a column of water to a region with higher or lower planetary vorticity.


Lecture
14: The Sverdrup balance and gyre circulation