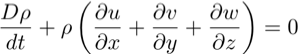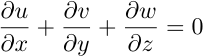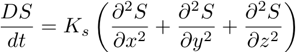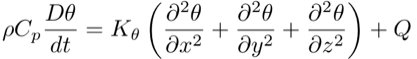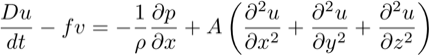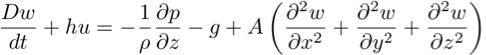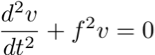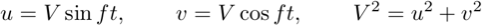Notes
1.
Mass Conservation Equation and Continuity
We
note that the first term, the change in density with time
(moving with a fluid parcel) is very small for time scales
larger than a few seconds. In other words, except for sound
waves, the compressibility of the water parcel is
unimportant and can be neglected. Hence we find the CONTINUITY
EQUATION,
which says that the divergence of the flow is zero - that
is, the flow is NON-DIVERGENT.
2.
Salt Conservation
The
equation for salt conservation can be developed similarly to
that for mass, but now we need to consider exchanges of salt
via diffusive fluxes. Diffusion acts on the gradient of
salinity.
where
K_s is the diffusion coefficient of salt. This is simplified
when we consider a non-divergent flow:
3.
Heat Conservation
Energy
has several forms in the ocean: kinetic and potential energies
(mechanical), internal energy, and chemical energy. We can
measure internal energy by measuring the temperature of the
fluid. Mechanical and chemical energy dissipation into heat is
small. By far the largest contribution to heat in the ocean
comes from solar radiation and the surface heat flux. Again,
we assume non-divergent flow.
where
Cp is the heat capacity of sea water and K_theta is the
diffusion coefficient for temperature (100x larger than K_s).
Q is the heating due to mechanical or chemical energy
dissipation (small), or due to heat exchange with the
atmosphere.
4.
Momentum Conservation and the Coriolis force
For
the conservation of momentum we must consider the advection of
momentum across the walls of our fluid parcel plus all
external forces on the parcel that may change its momentum, in
other words, all forces that can accelerate the flow. The
external forces are pressure gradients, gravity, and shear
stresses (in the form of eddy viscosity). We must also
consider the affect of ROTATION on the flow. In transforming
from an inertial (non-accelerating) frame to a rotating
(accelerating) frame, such as we live in here on earth, we
derive the CORIOLIS FORCE. For ocean circulation the time and
space scales of the flow are such that the Coriolis effect is
important.
There
are three momentum equations, one each for the u, v, and w
components of the flow.
where
and
A is the kinematic eddy viscosity (coefficient of viscosity
divided by density)
4.
Inertial Oscillations
Inertial
oscillations are motions in the ocean that occur in response
to an impulse force. Such a force could be a wind event, for
example, that sets the water in motion and then leaves it to
“restore” under the influence of only the Coriolis force. With
no external forces, the horizontal Equations of Motion become:
These
equations are coupled, first order, linear differential
equations and can be solved. If we re-arrange the second
equation and substitute it into the first we should recognise
the equation for a harmonic oscillator.
with
solution,
these
equations describe a circle of radius R = V/f and period, T =
2∏/f.
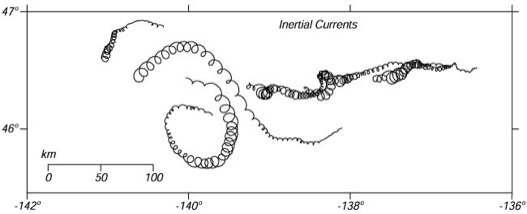
Inertial
currents are the most common motions in the ocean. They are
only a few kilometers in scale and decay in a few days.
Inertial
currents in the North Pacific in October 1987 (days 275-300)
measured by holey-sock drifting buoys drogued at a depth of
15 meters. Positions were observed 10-12 times per day by
the Argos system on NOAA polar-orbiting weather satellites
and interpolated to positions every three hours. The largest
currents were generated by a storm on day 277. Note: these
are not individual eddies. The entire surface is rotating. A
drogue placed anywhere in the region would have the same
circular motion. From van Meurs (1998).
Extra material:
Movie illustrating the Coriolis effect:
An
in-depth look at the Coriolis effect by Jim Price at MIT/WHOI:
Reading:
JK4-5,
PP4,6&10, OU3&6, RS7
Last
modified: Oct 2014

Lectures
7 & 8: Mass, salt, heat, and momentum conservation and the
Coriolis effect
The
way we understand the ocean is based on the simple concept of
CONSERVATION. If we consider an arbitrary volume of water, a
“parcel”, then over that volume mass must be conserved (it
cannot be created or destroyed). Temperature and salinity can
only change as a result of the flow of warmer/colder water or
saltier/fresher waters across the boundaries of the volume, or
due to the diffusion of temperature or salt into the volume.